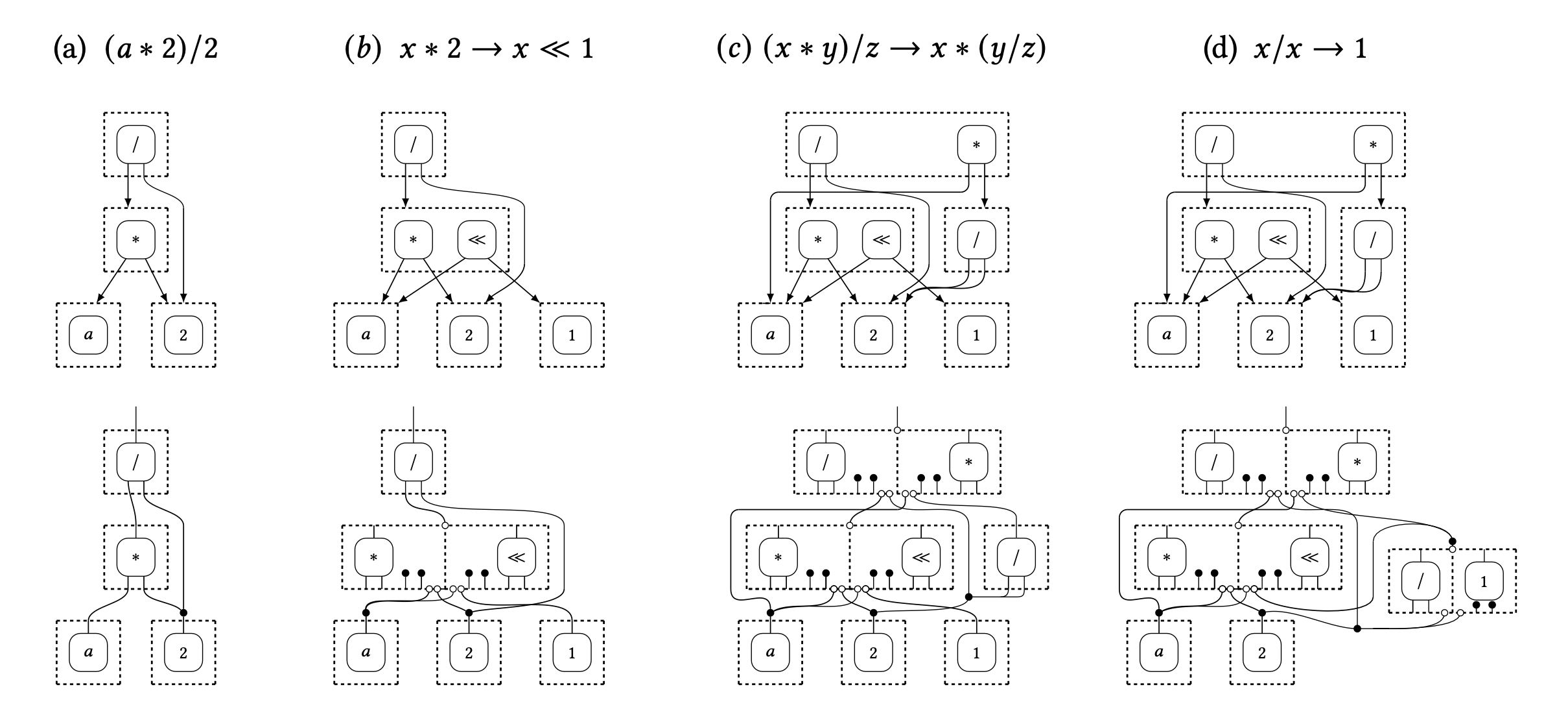
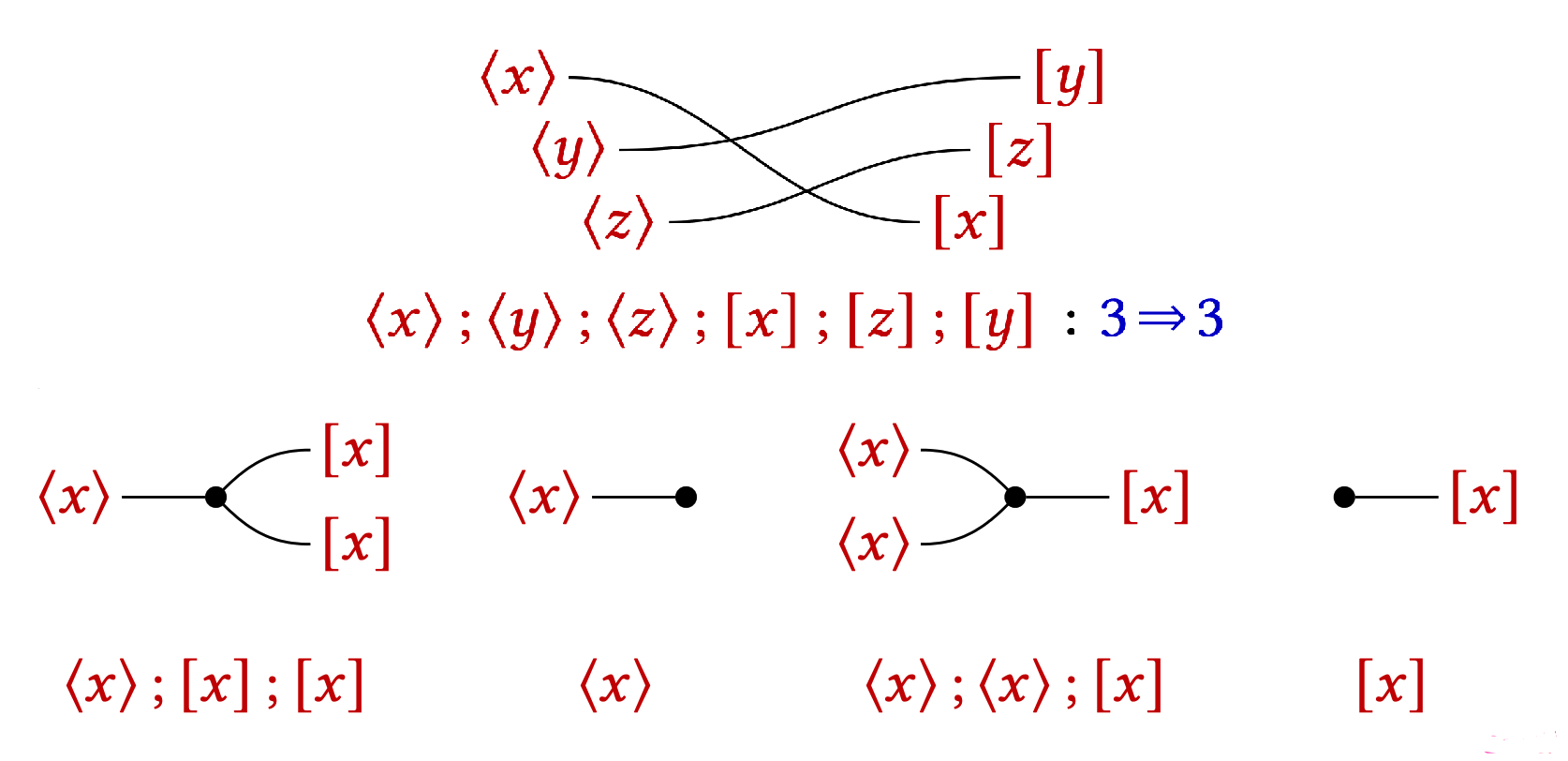
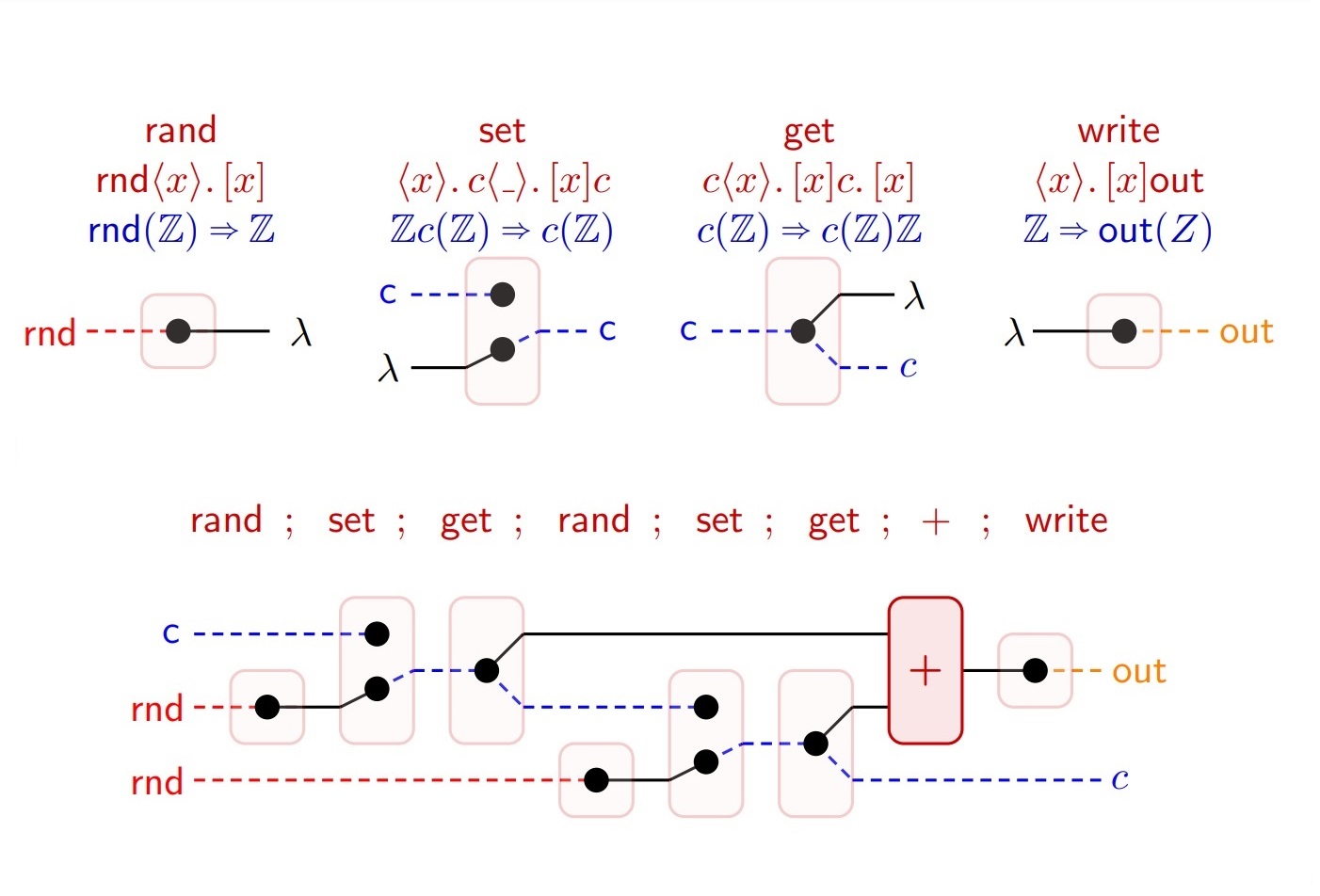
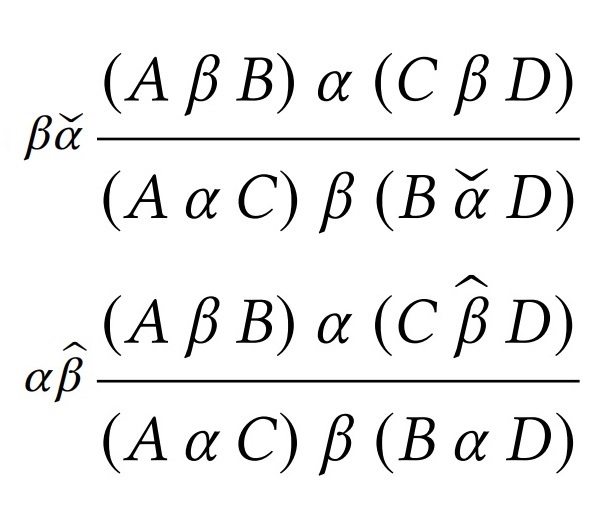Dr. Chris Barrett

I'm a programming languages and category theory researcher, currently working at Planting Space. Previously, I have held post-doctoral positions with Dr. Aleks Kissinger in the Quantum Group in the Dept. of Computer Science at the University of Oxford and with Dr Dan Ghica within the Theory of Computation group at the University of Birmingham. I received my Ph.D. in Theoretical Computer Science from the University of Bath in 2023, while working on Mathematical Foundations of Computation. My supervisor was Willem Heijltjes. My master's and undergraduate degree were in (pure) mathematics.

My research interests are in the area of proof and type theory, the lambda-calculus, and programming language semantics. I am especially interested in designing calculi and type systems for computational effects, including for quantum computation. My understanding of these subjects is influenced by deep inference and by (pure and applied) category theory.

I was sole organizer of the Bath Mathematical Foundations Seminar in the years 2020-2022, and co-organizer of the Birmingham Theory Seminar in 2023. I also worked as a teaching assistant at the University of Bath for modules in Foundations of Computation, Functional Programming, and Analytical Mathematics for Applications in the years 2018-2021.

ORCID iD | Google Scholar | LinkedIn | e-mail | CV

Research and Publications

The Relational Machine Calculus

Chris Barrett, Daniel Castle, Willem Heijltjes

Logic in Computer Science 2024

This paper presents the Relational Machine Calculus (RMC): a simple, foundational model of first-order relational programming. The core of the calculus is given by a decomposition of the first-order lambda-calculus which reveals a latent duality, concretely expressed by an involution on syntax. Semantically, this core fragment is sound and complete for string diagrams of Frobenius monoids. A corresponding symmetrization of beta-reduction gives rise to unification as a reduction mechanism. By further including standard operations of Kleene algebra the RMC embeds a range of computational models: the first-order lambda-calculus, logic programming, and automata, among others. These embeddings preserve operational semantics, which for the RMC is given by a generalization of a standard stack machine for the lambda-calculus. The equational theory of the RMC (which supports reasoning about its operational semantics) is conservative over both the first-order lambda-calculus and Kleene algebra, and can be oriented to give a confluent reduction relation.

Paper (Conference)

Equivalence Hypergraphs: E-Graphs for Monoidal Theories

Chris Barrett, Dan Ghica, Aleksei Tiurin

Publication TBC

The technique of equipping graphs with an equivalence relation, called equality saturation, has recently proved both powerful and practical in program optimisation. However, such structures, which are called e-graphs, apply only to certain kinds of theories, namely to algebraic theories where the generators have a single output which is inherent to what an abstract syntax tree is. The theories where the generators can have many inputs, as well as many outputs, are called monoidal theories. These theories have a wide area of applications, including quantum computing and digital circuits, which would benefit from having a corresponding e-graph machinery for them. We provide a generalisation of e-graphs for arbitrary monoidal theories through building a categorical construction. We argue that e-graphs themselves can be seen as a specific instance of this construction when applied to Cartesian monoidal theories. This not only paves the way for new applications but also lays a solid foundation for reasoning about e-graphs.

To be presented at EGRAPHS, a satellite workshop of Programming Language Design and Implementation 2024.

Paper (Arxiv)

The Functional Machine Calculus II: Semantics

Chris Barrett, Willem Heijltjes, Guy McCusker

Computer Science Logic 2023

The Functional Machine Calculus (FMC), recently introduced by Heijltjes, is a generalization of the lambda-calculus which may faithfully encode the effects of higher-order mutable store, I/O and probabilistic/non-deterministic input. Significantly, it remains confluent and can be simply typed in the presence of these effects. In this paper, we explore the denotational semantics of the FMC.

We have three main contributions: first, we argue that its syntax -- in which both effects and lambda-calculus are realised using the same syntactic constructs -- is semantically natural, corresponding closely to the structure of a Scott-style domain theoretic semantics. Second, we show that simple types confer strong normalization by extending Gandy's proof for the lambda-calculus, including a small simplification of the technique. Finally, we show that the typed FMC (without considering the specifics of encoded effects), modulo an appropriate equational theory, is a complete language for Cartesian closed categories.

Presented at the NIETS workshop and Computer Science Logic (CSL) 2023.

Paper (Conference) | Slides (NIETS'22, CSL'23)

A Subatomic Proof System for Decision Trees

Chris Barrett, Alessio Guglielmi

Transactions on Computational Logic 2022

We design a proof system for propositional classical logic that integrates two languages for Boolean functions: standard conjunction-disjunction-negation and binary decision trees. The system exhibits remarkable proof-theoretical naturalness: the system consists of all and only the inference rules generated by the single, simple, linear scheme of the recently introduced subatomic logic (pictured, right).

Thanks to this regularity, cuts are eliminated via a natural construction. By expanding the language of propositional logic, we make its proof theory more regular and generate more proofs, some of which are very efficient. That design is made possible by considering atoms as superpositions of their truth values, which are connected by self-dual, non-commutative connectives. To accommodate self-dual non-commutativity, we compose proofs in deep inference.

Presented at Structures and Deduction, a satellite workshop of FSCD 2019.

Paper (Journal) | Slides (S&D'19)

Ph.D. Thesis: On the Simply Typed Functional Machine Calculus: Categorical Semantics and Strong Normalisation

Thesis advisor: Willem Heijltjes

Department of Computer Science, University of Bath, December 2022

The Functional Machine Calculus (FMC) was recently introduced as a generalization of the lambda-calculus to include higher-order global state, probabilistic and non- deterministic choice, and input and ouput, while retaining confluence. The calculus can encode both the call-by-name and call-by-value semantics of these effects. This is enabled by two independent generalizations, both natural from the perspective of the FMC’s operational semantics, which is given by a simple (multi-)stack machine.

The first generalization decomposes the syntax of the lambda-calculus in a way that allows for sequential composition of terms and the encoding of reduction strate- gies. Specifically, there exist translations of the call-by-name and call-by-value lambda-calculus which preserve operational semantics. The second parameterizes application and abstraction in terms of ‘locations’ (corresponding to the multiple stacks of the machine), which gives a unification of the operational semantics, syn- tax, and reduction rules of the given effects with those of the lambda-calculus. The FMC further comes equipped with a simple type system which restricts and captures the behaviour of effects.

This thesis makes two main contributions, showing that two fundamental prop- erties of the lambda-calculus are preserved by the FMC. The first is to show that the categorical semantics of the FMC, modulo an appropriate equational theory, is given by the free Cartesian closed category. The equational theory is validated by a notion of observational equivalence. The second contribution is a proof that typed FMC-terms are strongly normalising. This is an extension (and small simplification) of Gandy’s proof for the lambda-calculus, which additionally emphasizes its latent operational intuition.

Presented at the Birmingham, Oxford and Cambridge University Theory seminars.

Thesis | Slides (Viva) | Slides (Birmingham, Oxford, Cambridge Theory Seminars '22/'23)

Masters' Project: On the Quantized Dynamics of Factorial Languages

Chris Barrett, Evgenios Kakariadis

The Quarterly Journal of Mathematics 2017

For my masters' project at Newcastle University I researched and wrote an introduction to Symbolic Dynamics, including some Haskell code to generate "follower set graphs" -- finite representations of certain spaces of infinite sequences. This code was used to falsify a conjecture and was part of my small contribution to the above published mathematics paper. The work was awarded the Best MMath Project school prize.